How BIP47 Works

BIP47, also known as Reusable Payment Codes for Hierarchical Deterministic Wallets, is a proposal by Justus Ranvier that enables us to create static payment codes. Unlike ordinary Bitcoin addresses, a BIP47 payment code is used between involved parties (sender and receiver) to generate a new address every time a payment is made, avoiding address reuse.
We’ll see in this article its use cases, how it works and write a little implementation using bcoin.

The inspiration for this text comes from the very nice BIP47, the ugly duckling, translated by Su Z from the original by Loïc Morel.

1. Use Cases

The most commonly mentioned use case is having donation addresses without reusing addresses. We all know reusing addresses is bad for privacy. Take a look, for example, at the bitaddress.org Web wallet generator. Anyone can see that the donation address in the footer has received since 2011 over 36 bitcoins. How bad things can get if people know someone owns all that money?

Another example is The Freedom Convoy by the Canadian truckers. Many of them received donations on a static address. Since their identities were known by the government and they sent their BTC to exchanges, some of them had their bitcoins seized. The address reuse was not the only mistake here, but the fact that the donation address was public was crucial for tracking the coins.
With a BIP47 reusable payment code, chain analysts wouldn’t have an address to track to begin with.

And last, one feature that is rarely mentioned is user experience (UX). Any banking app allows the user to save a contact and transfer money to him occasionally. In Bitcoin, though, there’s this cumbersome task of asking for a new address before each transaction. BIP47 makes it possible to save a contact in the wallet and generate a brand new address every time.
Check how it looks on Samourai and Sparrow wallets:

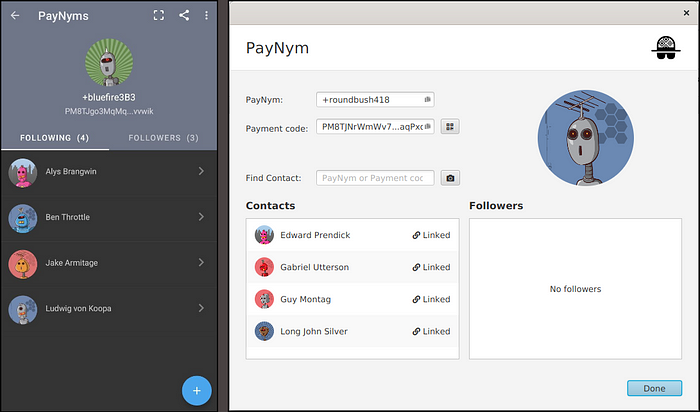
2. Summary

The procedure will be detailed in the following section, but here’s a brief summary of how it works. In the example, Alice is paying Bob:

1- Alice gets Bob’s payment code. Besides some metadata, this code contains Bob’s xpub at derivation path 47;

2- Alice prepares a notification transaction. She selects one of her UTXOs and creates a shared secret S = k.B, with k being the private key of one of her UTXOs and B being the first public key of Bob’s xpub.
She encrypts her own payment code applying XOR between her code and HMAC-SHA512(o, Sx), with o being the previous outpoint of the UTXO and Sx being the X coordinate of S;

3- She sends the transaction to Bob’s notification address, which is the first address of Bob’s xpub, including her encrypted payment code in the op_return;

4- Bob reads the op_return, finds S = b.K, with b being the private key of B and K being the public key of k. Bob gets K and o from the notification transaction. With that info, he is able to retrieve Alice’s payment code;

5- Alice can now derive new addresses and send payments to Bob by multiplying the private key a from her payment code and Bob’s public keys B0, B1, B2 etc from his payment code.
Bob will do the opposite: b0.A, b1.A, b2.A etc;

3. Implementation

Let’s create a directory called bip47 and init the node project with npm init. I am using node v16.19.0 here. We’ll be using the following libraries:

• bcrypto, for the secp256k1 operations;
• bs58, to decode base58;
• bcoin, as the Bitcoin library;

Install everything with:

$ npm i bcrypto@^5.4.0 bs58@^5.0.0 "git+https://github.com/bcoin-org/bcoin.git#semver:~2.0.0"

BIP47 specification is currently at version 4, but we will use version 1, since this is the only one currently implemented by wallets (Samourai and Sparrow). All code below will use the following imports:

const { Address, Coin, HDPrivateKey, HDPublicKey, KeyRing, MTX, Mnemonic, Network, Output, Script } = require("bcoin");
const { privateKeyTweakAdd, publicKeyTweakMul, publicKeyCombine } = require("bcrypto").secp256k1;
const bs58 = require("bs58");
const crypto = require("crypto");

3.1 Scenario

Alice wants to pay Bob using BIP47.
Her wallet has the random seed words life life life life life life life life life life life life and passphrase alice. BIP47 uses keys from the same level as BIP44/49/84, but at path 47. Let’s get the xprv:

let aliceMasterKey = HDPrivateKey.fromMnemonic(new Mnemonic("life ".repeat(12).trim()), "alice");
let aliceXprv = aliceMasterKey.derivePath("m/47'/1'/0'"); // for mainnet, m/47'/0'/0';

Alice then gets Bob’s payment code. Maybe she got the code from the donation page of his project. Or they’re just friends and frequently pay each other and she got tired of asking for a new address every time, so Bob sent her the code. This is the code:

PM8TJYp8zHvhimVNRjUcEuULfmvmUML6YTbTSnBuU69MYy93AzsXELFLaVjpxc5mxDex7R8ttgtL1tGAt2TshZAoFeB5zn4c9nRo4oZpmuyuo4FTpUrd

3.2 Payment Code

Let’s decode and print this code…

let bobCode = "PM8TJYp8zHvhimVNRjUcEuULfmvmUML6YTbTSnBuU69MYy93AzsXELFLaVjpxc5mxDex7R8ttgtL1tGAt2TshZAoFeB5zn4c9nRo4oZpmuyuo4FTpUrd";
bobCode = Buffer.from(bs58.decode(bobCode));
console.log(bobCode.hexSlice());
// 470100032a3f6b7e3a66a09f331fbaeaf8f8a52dd339f8db61af71ac07d00958b50e9bd73a463eda3da82bfc176ad4e8a386a736d56311296a2d2f6255a7723763e1bd4900000000000000000000000000a1b57782

…so that we can analyze it:

47 - prefix
01 - version
00 - features bit field
032a3f...0e9bd7 - public key
3a463e...e1bd49 - chaincode
000000...000000 - padding
a1b57782 - checksum

• Prefix: the 0x47 is fixed and becomes a “P” in base58check;
• Version: BIP47 version. Can be from 1 to 4. Current wallets implement version 1;
• Features bit field: this specifies an alternate notification method using the Bitmessage protocol. No wallets implement this, so currently it’s always zero;
• Public key: 33 bytes of the public key;
• Chaincode: 32 bytes of the chaincode;
• Padding: this field is actually reserved for future updates. If not used, it’s zero-filled up to 80 bytes;
• Checksum: 4 bytes for the base58check checksum;

The relevant parts here for Alice are the public key and the chaincode, which form a xpub. This is Bob’s xpub for path 47:

let bobXpub = new HDPublicKey();
bobXpub.publicKey = bobCode.subarray(3, 36);
bobXpub.chainCode = bobCode.subarray(36, 36 + 32);

This snippet ignores all bytes but the xpub ones. A real wallet should, of course, check the version and checksum.

3.3 Notification Transaction

Now Alice needs to send her payment code to Bob. She first derives Bob’s notification address, which is the first address of his xpub:

const network = Network.get("testnet");
let notifPubkey = bobXpub.derive(0).publicKey;
let pkh = crypto.createHash('ripemd160').update(crypto.createHash('sha256').update(notifPubkey).digest()).digest();
let notifAddr = Address.fromScript(Script.fromPubkeyhash(pkh));
console.log(notifAddr.toBase58(network));
// mkGw3ojQ88R7mN6RW1LENXXu12aAvwqavy

To send the transaction, one or more coins are of course needed. Any UTXOs can be selected here. The only requirement by BIP47 is that the key(s) chosen mustn’t be easily associated to Alice’s own payment code.

If an observer that sees the notification transaction is able to identify Alice as the sender of the transaction, then he will deduce Alice is probably making payments to Bob.

Her wallet is going to write her payment code in the op_return of the notification transaction. Since we don’t want other to see the payment code, her wallet will encrypt it. Thanks to Elliptic-curve Diffie–Hellman (ECDH), two parties can share a secret without having to share an encryption key.

Basically, a.B = B.a, with a and A being Alice’s private and public keys and b and B being Bob’s. Let’s test if this is indeed true (the following code uses node’s REPL and is independent from our main code):

> sec = require("bcrypto").secp256k1;
> priv1 = sec.privateKeyGenerate()
< Buffer 12 51 40 00 13 db e2 76 b3 d5 99 af 7e 80 2a 8b 75 f1 30 86 97 81 36 ea 83 c1 d6 da 8f 2a 08 f0 >
> pub1 = sec.publicKeyCreate(priv1)
< Buffer 03 30 b0 39 45 51 94 07 a3 5f 65 24 68 a0 5a 25 a8 a8 7c 0c 7f 33 97 7d a5 00 d6 94 a2 b3 1c 25 88 >
> priv2 = sec.privateKeyGenerate()
< Buffer c9 4d fd 10 3e 71 e3 67 bc 0a e8 0e 99 09 9e fb 87 d6 b7 93 e9 a2 4b 73 33 99 1d ed bc 2a 70 81 >
> pub2 = sec.publicKeyCreate(priv2)
< Buffer 03 05 b8 5d df 51 e5 c3 b7 24 b5 4b a0 c5 c7 3d a4 33 d4 4b d9 f9 9d 7e 92 0e dd 43 ef 65 0b e3 5f >
> sec.publicKeyTweakMul(pub1, priv2).equals(sec.publicKeyTweakMul(pub2, priv1))
true

So, Alice’s wallet will select one UTXO and calculate a shared secret S using the private key of this UTXO and Bob’s notification address public key. Then, it will calculate the HMAC-SHA512 of the X coordinate of S and the previous outpoint prevOut of her UTXO, also known as the blinding factor.

The first half of the result will be used to encrypt the public key of her payment code and the second half will encrypt the chaincode. XOR will be used for both operations.

Confusing, huh? Let’s see that in practice. Alice has 19,000 satoshis on tb1qh9y89qjjymappx2fm2j3ah9yz8na0yw2u9vqk6. That’s enough to pay for the notification transaction, hence that UTXO is selected. If further UTXOs were needed, only data from the first one would be used to encrypt the payment code.

let utxoPrivkey = KeyRing.fromSecret("cUXoUxNatN3M8QCaK9SYctdijvhPQyxuxcFjXXv6Xu7i7PiCTJtg");
utxoPrivkey.witness = true;
utxoPrivkey.refresh();
let S = publicKeyTweakMul(notifPubkey, utxoPrivkey.getPrivateKey());

Alice has calculated the shared secret S = k.B. She also needs the previous outpoint of the UTXO (little endian):

let prevTxidLE = Buffer.from("afe546259680de75265219f6172c4f980b1f18439b5c1d2ca10497394b2890a3", "hex").reverse();
let prevIndex = 0;
let prevIndexLE = Buffer.alloc(4);
prevIndexLE.writeInt32LE(prevIndex);
let prevOut = Buffer.concat([prevTxidLE, prevIndexLE]);

Time to calculate the blinding factor f, which uses the X coordinate of S and the outpoint…

let Sx = S.subarray(1);
let f = crypto.createHmac("sha512", prevOut).update(Sx).digest();
let f1 = f.subarray(0, 32);
let f2 = f.subarray(32);

…to finally XOR encrypt the public and chaincode of Alice’s xprv, which we already got up there. Note only the X coordinate is encrypted. That’s why the Y coordinate is later prepended to finish the encrypted xpub.
And finally, after addding the version, bitmessage and padding, the payload is ready to be included in the op_return.

let aliceCodePubkey = aliceXprv.publicKey;
let aliceCodeChaincode = aliceXprv.chainCode;

let encryptedPublickeyX = f1.map((byte, i) => byte ^ aliceCodePubkey.subarray(1)[i]);
let encryptedChaincode = f2.map((byte, i) => byte ^ aliceCodeChaincode[i]);
let publicKeyY = aliceCodePubkey.subarray(0, 1);
let encryptedXpub = Buffer.concat([publicKeyY, encryptedPublickeyX, encryptedChaincode]);
let encryptedPayload = `0100${encryptedXpub.hexSlice()}`.padEnd(160, "0");

Let’s assemble the notification transaction. First, we’ll create the transaction and its input:

const coinValue = 19000;
let coin = new Coin();
coin.hash = prevTxidLE;
coin.index = prevIndex;
coin.value = coinValue;
coin.script = Script.fromAddress(utxoPrivkey.getAddress().toBech32(network));
let mtx = new MTX();
mtx.addCoin(coin);

The transaction will have three outputs. First, the op_return containing the encrypted payload we have already created.

Then, an output to Bob’s notification address, which will tell Bob’s wallet someone has opened a channel with him. It can have any value, but the minimum relayed by Bitcoin Core currently is 546 sats.

Finally, the change output, if any:

let nulldata = Output.fromScript(Script.fromNulldata(Buffer.from(encryptedPayload, "hex")), 0);
mtx.addOutput(nulldata);

const dust = 546;
mtx.addOutput({
  address: notifAddr,
  value: dust
});

const minerFee = 250;
mtx.addOutput({
  address: "tb1qwuq6p25zpqey9rhszv78hgd5fd38ang0xe6j6n",
  value: coinValue - dust - minerFee
});

console.log(`Inputs signed: ${mtx.sign(utxoPrivkey)}`);
// Inputs signed: 1
console.log(mtx.toTX().toRaw().hexSlice());
// 01000000000101a3...2be32d7c00000000

The notification transaction is pushed. Bob’s wallet notices the transaction and obtains Alice’s payment code (more on that later). Independently from Bob’s Wallet, Alice can start making payments to Bob.

3.4 Payment Transaction

Deriving payment addresses is simple. From Bob’s xpub, for the first payment, Alice’s wallet will derive the public key at index zero (which is the same from his notification address), called here B0. For the following payments, she’ll use index 1, 2 and so on. These public keys will be multiplied by her notification private key a to calculate a shared secret S, so that S0 = a.B0, S1 = a.B1 etc.
Then, the sha256 of the X-coordinate of public key S will be calculated to obtain a new scalar s.

With s and G, the generator point of the secp256k1 curve, we obtain a new point sG = s.G, to finally get the address public key K0 = B0 + sG. It looks complicated, but it’s actually just a few lines of code:

const G = Buffer.from("0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798", "hex");

let a = aliceXprv.derive(0).privateKey;
for (let index = 0, addrCount = 0; addrCount <= 5; index++) {
  try {
    let B = bobXpub.derive(index).publicKey;
    let S = publicKeyTweakMul(B, a);
    let Sx = S.subarray(1);

    let s = crypto.createHash('sha256').update(Sx).digest();
    let sG = publicKeyTweakMul(G, s);
    let K = publicKeyCombine([B, sG]);
    let pkh = crypto.createHash("ripemd160").update(crypto.createHash("sha256").update(K).digest()).digest();
    let paymentAddr = Address.fromScript(Script.fromProgram(0, pkh));

    addrCount++;
    console.log(`Address #${index}: ${paymentAddr.toBech32(network)}`);
    } catch (e) {
      continue;
    }
}

I’ve added addrCount and surrounded everything with the try/catch block because those key multiplication and addition can produce keys outside the curve and those should be skipped. Here’s the output:

Address #0: tb1q8gpaft5rpju8lcshfa6at44pev5y0q7kzfwqpg
Address #1: tb1qes6funanqdkwk39zfwmzfnjuz3xt6apeltyhv5
Address #2: tb1q82pufc4zyhdtzemuqlaf2f2tgsy5jex6xf20r0
Address #3: tb1qmgdad8lwvm96grz5dy5yppmt5nxk5g38jftz8d
Address #4: tb1qdku0qjt7jy9hu6k5nt88sk52ddlzl6pnkg64m7
Address #5: tb1qzjpdp37nr8wf8qsysk28ph8e2xzhcv0pr2r6u3

BIP47 doesn’t mention SegWit addresses because it was created before SegWit was a thing, but the implementing wallets do use them.
To test, I’ve sent a transaction to the first address and it did show up on a Samourai wallet. Since we didn’t use the PayNyms directory, it displays the payment code instead of Alice’s nym:

3.5 Receiving the Notification Transaction

So, how does Bob access the coins Alice has sent him? Well, his wallet was monitoring outputs to his notification address. As soon as it identifies the notification transaction, it retrieves Alice’s encrypted payment code in the op_return.
It also obtains the public key of Alice’s UTXO and its previous outpoint:

let txCode = Buffer.from("0100036c11d62dc5d47a03edf9027dc045406f81da1bf89e701c3ac691468ecb154661d7e65b9aa400701c44f396b627e8592bbb081764d92df98ebce9a8a3b9360dfc00000000000000000000000000", "hex");
let txPublicKey = Buffer.from("02a7a6edc3de4e35ab54f98b69bedace05cc649e0dc51c7dfdeabe0db42be32d7c", "hex");
let txTxidLE = Buffer.from("afe546259680de75265219f6172c4f980b1f18439b5c1d2ca10497394b2890a3", "hex").reverse();
let txPrevIndex = 0;
let txPrevIndexLE = Buffer.alloc(4);
txPrevIndexLE.writeInt32LE(txPrevIndex);
let txPrevOut = Buffer.concat([txTxidLE, txPrevIndexLE]);

Now Bob has to calculate the same shared secret S Alice has used. She did S = k.B. Bob just got K from the transaction input, so he does S = b.K:

let bobMasterKey = HDPrivateKey.fromMnemonic(new Mnemonic("life ".repeat(12).trim()), "bob");
let bobXprv = bobMasterKey.derivePath("m/47'/1'/0'");
let notifPrivkey = bobXprv.derive(0).privateKey;
S = publicKeyTweakMul(txPublicKey, notifPrivkey);

Yeah, Bob has the same random seed words as Alice. Luckily, his passphrase bob makes it a completely new wallet. He then calculates the blinding factor f the same way Alice did and applies XOR to her encrypted payment code, retrieving her real payment code:

Sx = S.subarray(1);
f = crypto.createHmac("sha512", txPrevOut).update(Sx).digest();
f1 = f.subarray(0, 32);
f2 = f.subarray(32);

let encryptPubkey = txCode.subarray(2, 35);
let encryptCC = txCode.subarray(35, 35 + 32);

let aliceX = f1.map((byte, i) => byte ^ encryptPubkey.subarray(1)[i]);
let aliceCC = f2.map((byte, i) => byte ^ encryptCC[i]);
let aliceY = encryptPubkey.subarray(0, 1);
let alicePubkey = Buffer.concat([aliceY, aliceX]);

let aliceXpub = new HDPublicKey();
aliceXpub.publicKey = alicePubkey;
aliceXpub.chainCode = aliceCC;

3.6 Receiving the Payment Transactions

Remember how Alice derived payment addresses? For each index, she first calculated S = a.B, then got s = sha256(Sx) and finally the public key K = B + s.G.
Bob will perform S = b.A, then s = sha256(Sx) and finally k = b + s:

let A = aliceXpub.derive(0).publicKey;
for (let index = 0, addrCount = 0; addrCount <= 5; index++) {
  try {
    let b = bobXprv.derive(index).privateKey;
    let S = publicKeyTweakMul(A, b);
    let Sx = S.subarray(1);

    let s = crypto.createHash('sha256').update(Sx).digest();
    let k = privateKeyTweakAdd(b, s);
    let keyRing = KeyRing.fromPrivate(k);
    keyRing.witness = true;
    keyRing.refresh();

    addrCount++;
    console.log(`Address #${index}: ${keyRing.getAddress().toBech32(network)}`);
    console.log(`Privkey #${index}: ${keyRing.toSecret(network)}`);
  } catch (e) {
    continue;
  }
}

Note how Bob is the only person that can access the private keys, since Alice doesn’t know b. This is the output:

Address #0: tb1q8gpaft5rpju8lcshfa6at44pev5y0q7kzfwqpg
Privkey #0: cNHoo7PDFtjAuct2YNnUMYbWipXu4FDe2UsAm6h9Pc7GzUjm5kFb
Address #1: tb1qes6funanqdkwk39zfwmzfnjuz3xt6apeltyhv5
Privkey #1: cUH8sTdNjNE9b3LZ2JvbCuhJsCfF4HSpnW1R5NJRei1CrcGt318G
Address #2: tb1q82pufc4zyhdtzemuqlaf2f2tgsy5jex6xf20r0
Privkey #2: cT2kz7BrJoGgDatpasLQXxMTsCjmWAzp6orfNqz9SEVb76H1XHtx
Address #3: tb1qmgdad8lwvm96grz5dy5yppmt5nxk5g38jftz8d
Privkey #3: cVo5BmBptm6V86Bn42k1orRVKub9e5Fhpps8Ty6vQSiU4XGye8gr
Address #4: tb1qdku0qjt7jy9hu6k5nt88sk52ddlzl6pnkg64m7
Privkey #4: cPrnmc2JrFGk8M6kDyTG6snvotEoRhJYSCvR5RCQYZW676BHKSg9
Address #5: tb1qzjpdp37nr8wf8qsysk28ph8e2xzhcv0pr2r6u3
Privkey #5: cRMZVGG9EVFcKfRCVwdSsWgbeg8B49Qozimsdub4NzRPtLghS3DY

4. Conclusion

I had trouble in the past when I tried to understand how BIP47 worked by reading the BIP and references prior to the one mentioned in the introduction.

Hopefully this text helps to clarify how it works and possibly help wallet developers that want to implement it.